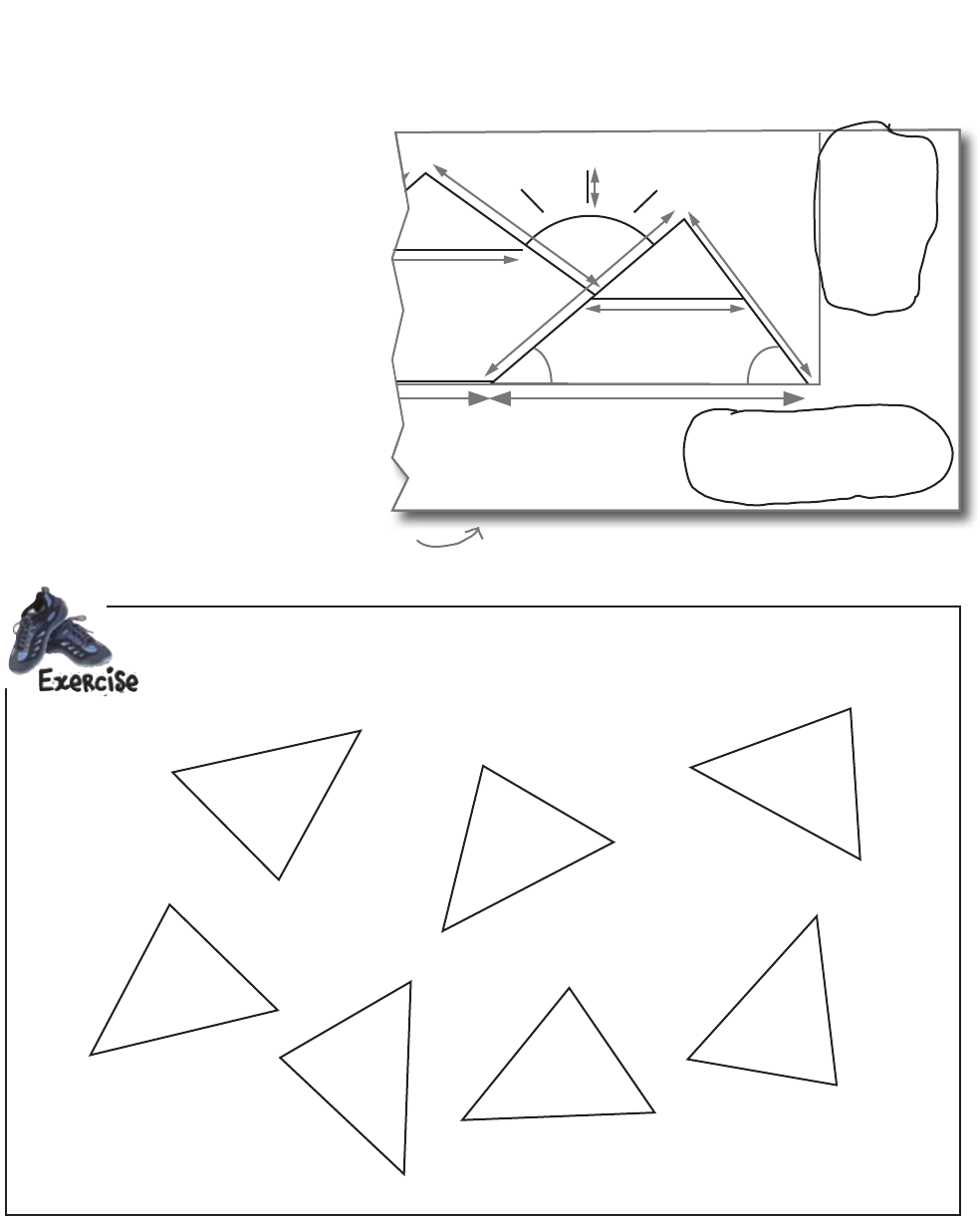
Y
ou can tell these ar
e the
same angle, ev
en bef
ore y
ou
work out wha
t tha
t angle is.
spotting similar triangles
Circle the triangles below that you can be SURE are similar to the triangle repeated
in the design.
53
o
86
o
53
o
41
o
86
o
53
o
53
o
41
o
41
o
53
o
86
o
86
o
41
o
86
o
41
o
You can spot similar triangles based on
just two angles
We know that angles in a triangle add up to 180 degrees, so once
you’ve got two angles in each triangle, you can always work out the
third.
And if you’ve noticed that two angles in one triangle are equal to two
angles in another triangle, then you can tell the triangles are similar
without even doing any math!
41
o
86
o
Look for two
equal angles
to spot similar
triangles.
41
o
86
o
62 Chapter 2
similarity and congruence
Q:
What if the triangles are flipped, so one has a 41° on the
right and the other has a 41° angle on left? Are they similar?
A:As long as you can spot another angle which is in
both triangles then yes, they’re definitely similar. Similarity is
maintained even if your shape is reflected or rotated.
Q:
Isn’t using similarity kind of like cheating? Shouldn’t I
be working out all the angles individually?
A:Cheating? We like to think of it as working smarter rather
than harder. It does save you plenty of leg work though. Most
geometry teachers will be more impressed by use of similarity
than repetitive calculations anyway—just make sure to make a
note on your work that you used similarity.
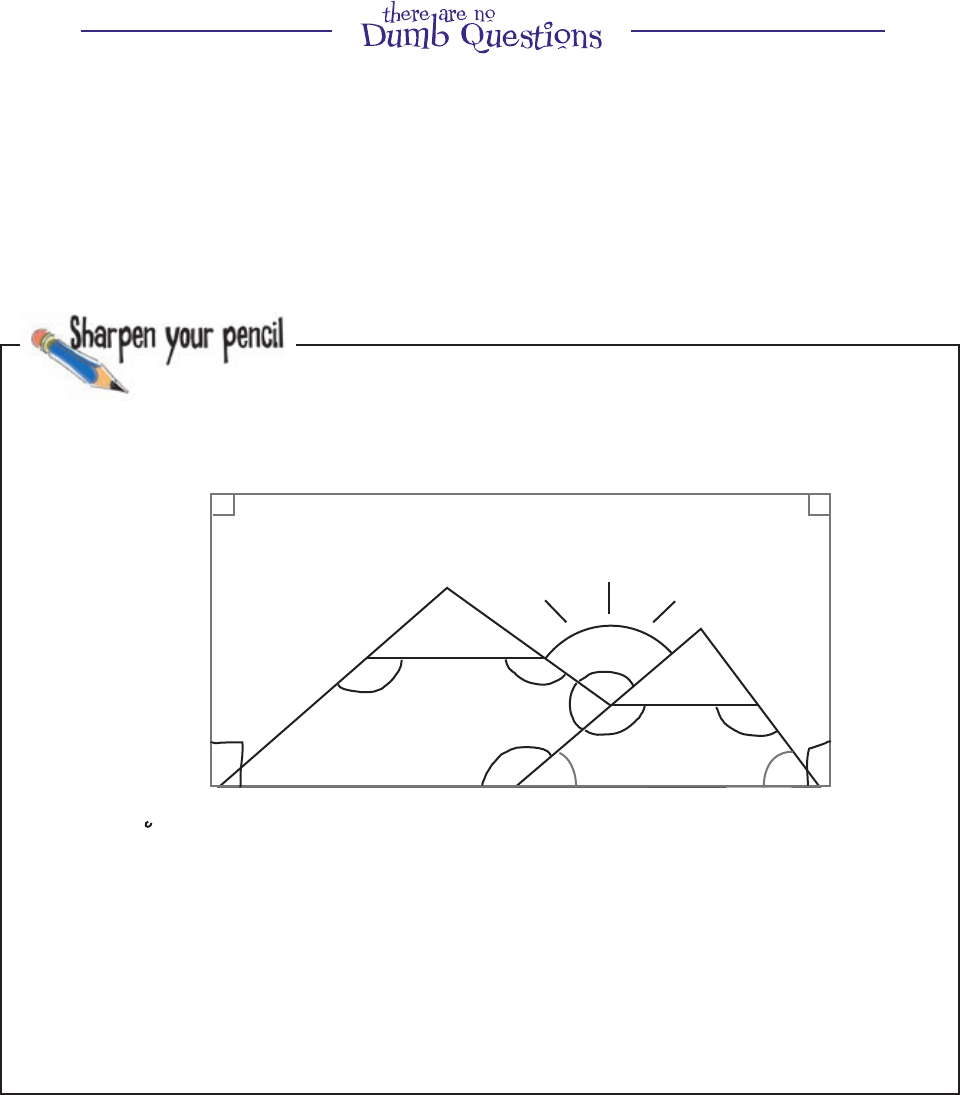
How many repeated angles are there in total on this diagram,
including the ones you’ve already marked plus the angles a
through i? (Count each value once—if it’s repeated don’t count it
again.)
41º 53º
86º
86º
41º
41º
41º
53º
53º
a
c
e
d
i
f
g
b
This corner a
lso
90
b
you are here 4 63
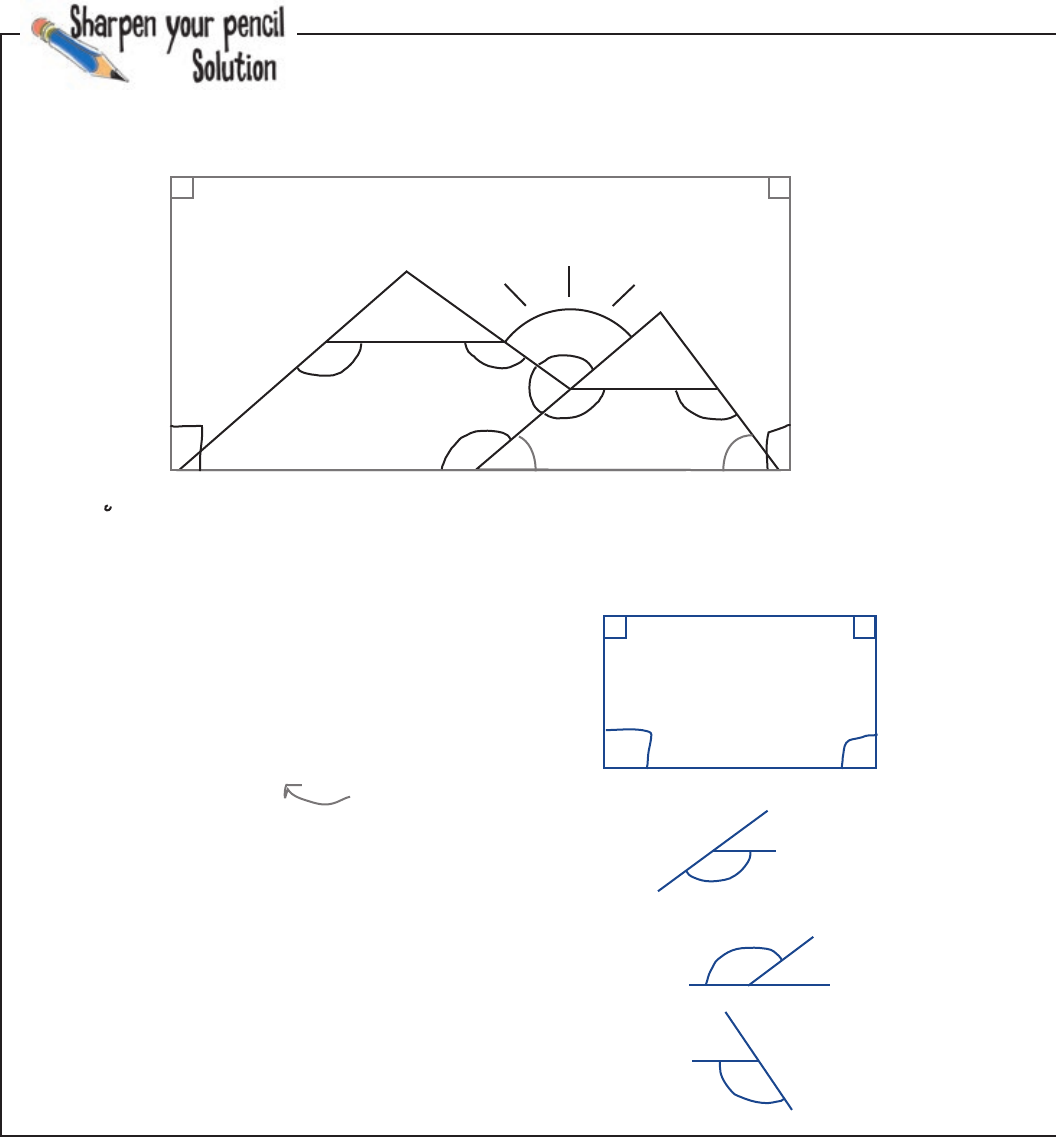
sharpen solution
a) The diagram tells us angle a is 90
o.
b) angle b completes the four-sided shape, so it must be
360
o
- (90
o
+ 90
o
+ 90
o)
=
90
o
c) angle c is on a straight line with 41
º
, so C = 180º - 41º = 139º
d) angle d is also on a straight line with 41º, so d = 180º - 41º = 139º
e) angle e is on a straight line with 53º, so e = 180º - 53º = 127º
90
o
b
41º
41º
53º
C
d
e
How many repeated angles are there in total on this diagram,
including the ones you’ve already marked, plus the angles a
through i? (Count each value only once—if it’s repeated don’t count
it again.)
Angles in a four-sided s
hap
e
a
lw
ays add up t
o 360º.
41º 53º
86º
86º
41º
41º
41º
53º
53º
a
c
e
d
i
f
g
b
This corner a
lso
90
b
64 Chapter 2
A bunch are r
ep
eated, r
ight? W
er
e
y
ou sur
pr
ised?
Z s
hap
e bet
w
een
para
llel lines
because they ar
e a
t the same
angle: 41º.
T
hese two s
hap
es
sets of matching angles.
similarity and congruence
Different angles: 90
º
, 41
º
, 53
º
, 86
º
, 127
º
, 139
º
, 94
º
… = 7 different angles in total
Repeated angles: 90
º
, 41
º
, 53
º
, 86
º
, 127
º
, 139
º
… = 6 angles are repeated
f) The left sides of the two mountains are both at 41
º
,
so they must be parallel. This means that angle f makes a
Z shape (alternate angles) with the 86
º
peak, so f must
also be 86
º
.
86º
f
T
hese two lines are parallel
g) by similarity, angle g must be the same as angle C, so g = 139
º
ar
e simil
ar, so their
angles ar
e the same!
T
hose li
ttle tick mark
s show
h) by similarity, angle i must be the same as angle e, so i = 127
º
i) angle i is on a straight line with f, which is 86
º
, so h = 180
º
- 86
º
= 94
º
you are here 4 65
Get Head First 2D Geometry now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

