
bring in the band
Liz is back with a special request
The great thing about happy customers is that they just keep
coming back. Impressed by the effort you put in to getting her
phone just right, Liz is trusting you with another great gig.
All the arr
ows ar
e the same.
The squ
are par
t is ha
lf the
length of the arr
ow head par
t.
T
ria
ngle sides ar
e the same.
The darker set of arr
ows ar
e
3/4 size.
Hey! Everyone thinks my phone
looks great. Can you do a totally
custom design on my brother’s
iPod of his band’s logo?
T
he sketch is pretty…er…sketch
y.
Drawn on the back of a fly
er by
the drummer.
An “arrow” is
one of these.
78 Chapter 2
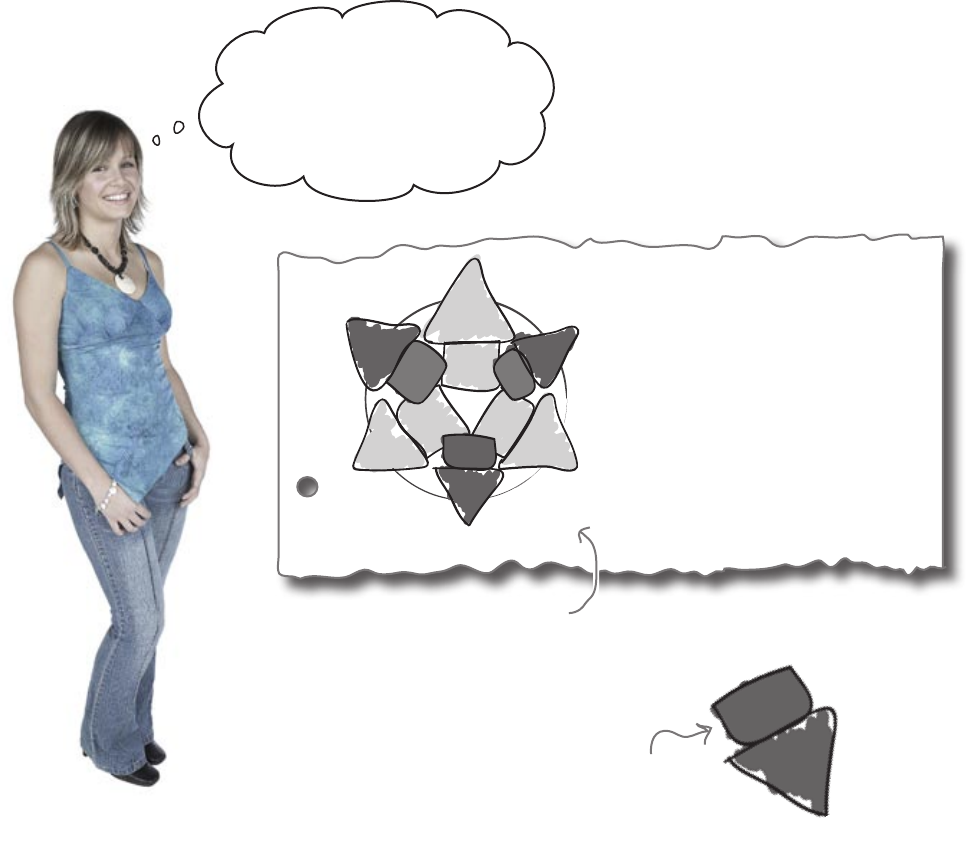
similarity and congruence
Before you start sketching the design, what lengths and angles
do you need to find? Could you use similarity to save yourself
some time and effort?
you are here 4 79

the arrows are similar
All the arr
ows ar
e the same.
The squ
are par
t is ha
lf the
length of the arr
ow head par
t.
T
riangle sides ar
e the same.
The darker set of arr
ows ar
e
3/4 size.
Although there aren’t any length or angle markings on the diagram,
the instructions give us plenty of clues—and there’s a ton of
similarity going on here.
T
he diagram is made up of six
simil
ar arrow shap
es like this.
A tr
iangle wi
th
thr
ee sides a
ll the
same length.
A squar
e wi
th sides
ha
lf the length of
the triangle sides.
This kind of tr
iangle is known as an
equila
teral tr
iangle (the note says
the thr
ee sides are the same), and
a
ll thr
ee angles ar
e the same as w
ell.
180
o
/3 = 60
o
There ar
e thr
ee large arrows
and thr
ee sma
ller ones, 3/4
of the size of the l
arge ones.
Before you start sketching the design, which lengths and angles
do you need to find? Could you use similarity to save yourself
some time and effort?
We need to find the lengths and angles of the sides of one of the
small triangles and one of the big triangles, plus the lengths of the
sides of one of the small squares and one of the big squares.
80 Chapter 2
Get Head First 2D Geometry now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

