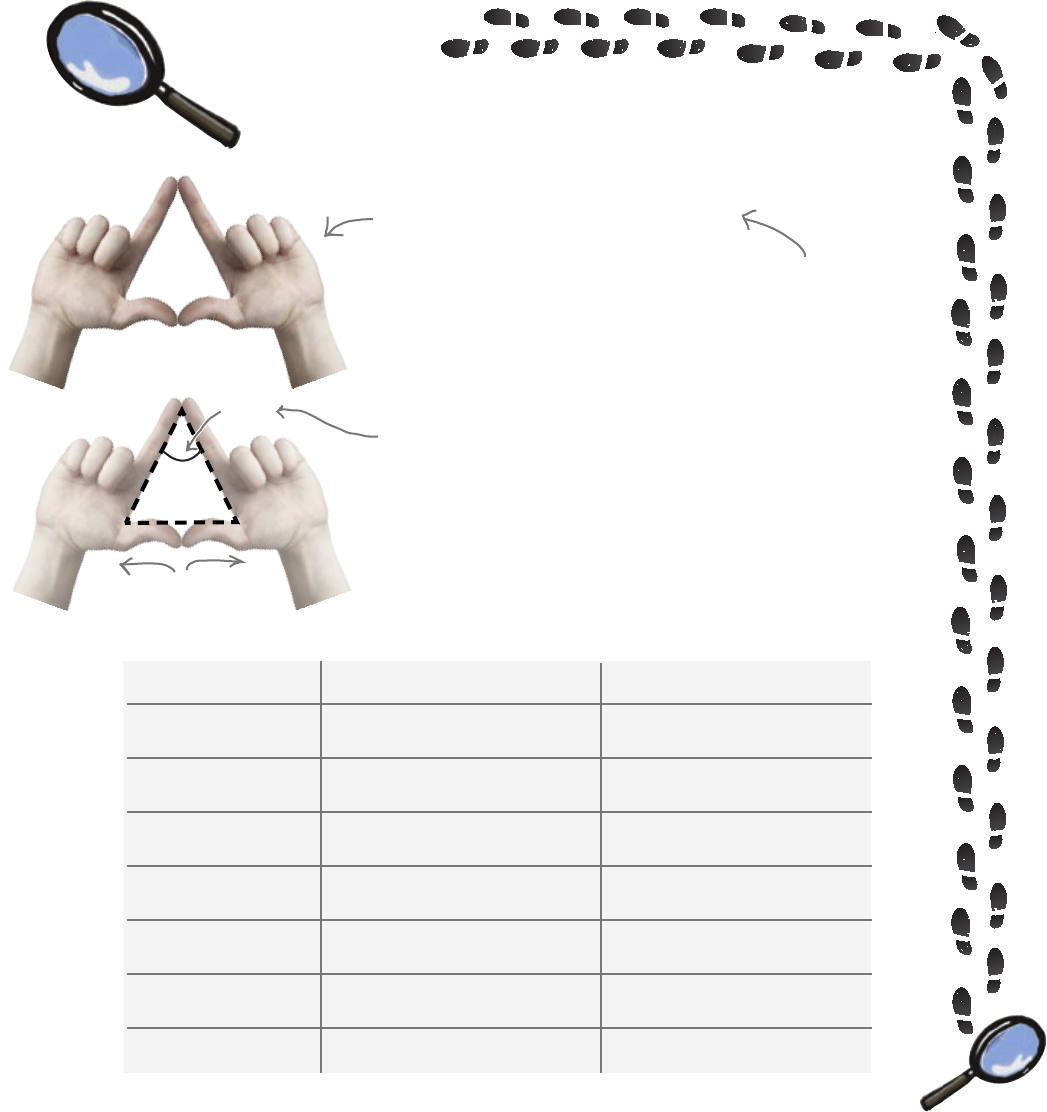
these rows.
v
a
lue gets rea
l close t
o the thing it’s nearl
y
equa
l t
o, but nev
er qui
te gets ther
e.
W
e a
lr
eady know ev
erything w
e need t
o,
bef
or
e w
e ev
en compar
e height and base,
but w
e found on page 167 that the height
w
as 75m, so tha
t a
lso fi
ts wi
th this row.
you’ve got the right speakers
The 60
o
speakers are spot on
We know that the sides of the field are longer than the base.
While this doesn’t allow us to say exactly what the apex angle
is—23º or 57º or something else—it does tell us that the apex
angle must be less than 60º. That means the 60º speakers
are ideal.
85m
85m
Field B
T
he side is longer
than the base...
80m
…so the tr
iangle is in
If apex angle is Sides and base Height and base
Almost 0º
Less than 60º
Exactly 60º
Between 60º and 90º
Exactly 90º
More than 90º
Almost 180º
Side ........................... base
Side ........................... base
Side ........................... base
Side ........................... base
Side ........................... base
Side ........................... base
Side ......................... 1/2 base
Height ......................... base
Height .........................1/2 base
Height .........................1/2 base
Height .........................1/2 base
Height .........................1/2 base
Height .........................1/2 base
Height ............................... 0
Greater than
Greater than
Equal to
Less than
Less than
Less than
Nearly equal to
Nearly equal to
Greater than
Greater than
Greater than
Equal to
Greater than
Less than
Math geek
s call this “approaching”—the
178 Chapter 4
triangle properties
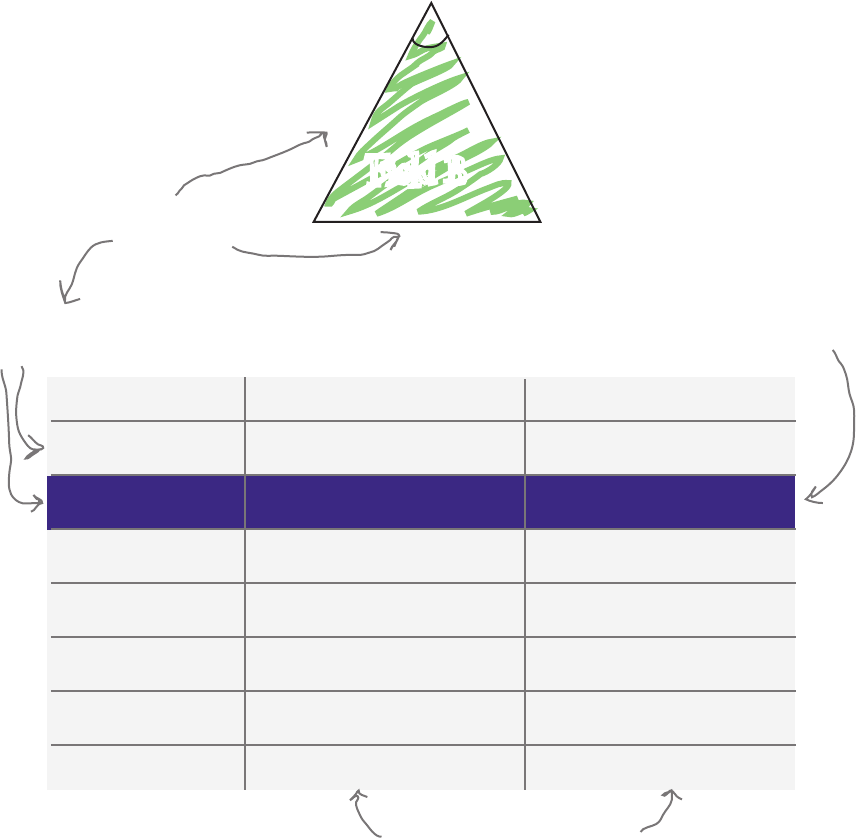
Estimating Angles Up Close
b
s
s
h
T
his is the
base.
T
hese are the
sides—they’r
e
equa
l.
T
he a
ltitude
on the base
giv
es us the
height.
T
his angle,
opposi
te the
base, is the one
w
e’r
e es
tima
ting.
In an equil
a
tera
l
triangle y
ou can’t tell
the base f
rom the
sides…that’s OK!
Don’t try to use
this on a sca
lene
tr
iangle!
aº
T
he sides can never
be less than ha
lf
the base.
For an isoceles triangle you can use the relative values of
the base, the sides, and the height to find out roughly what
the apex angle (the one opposite the base) is.
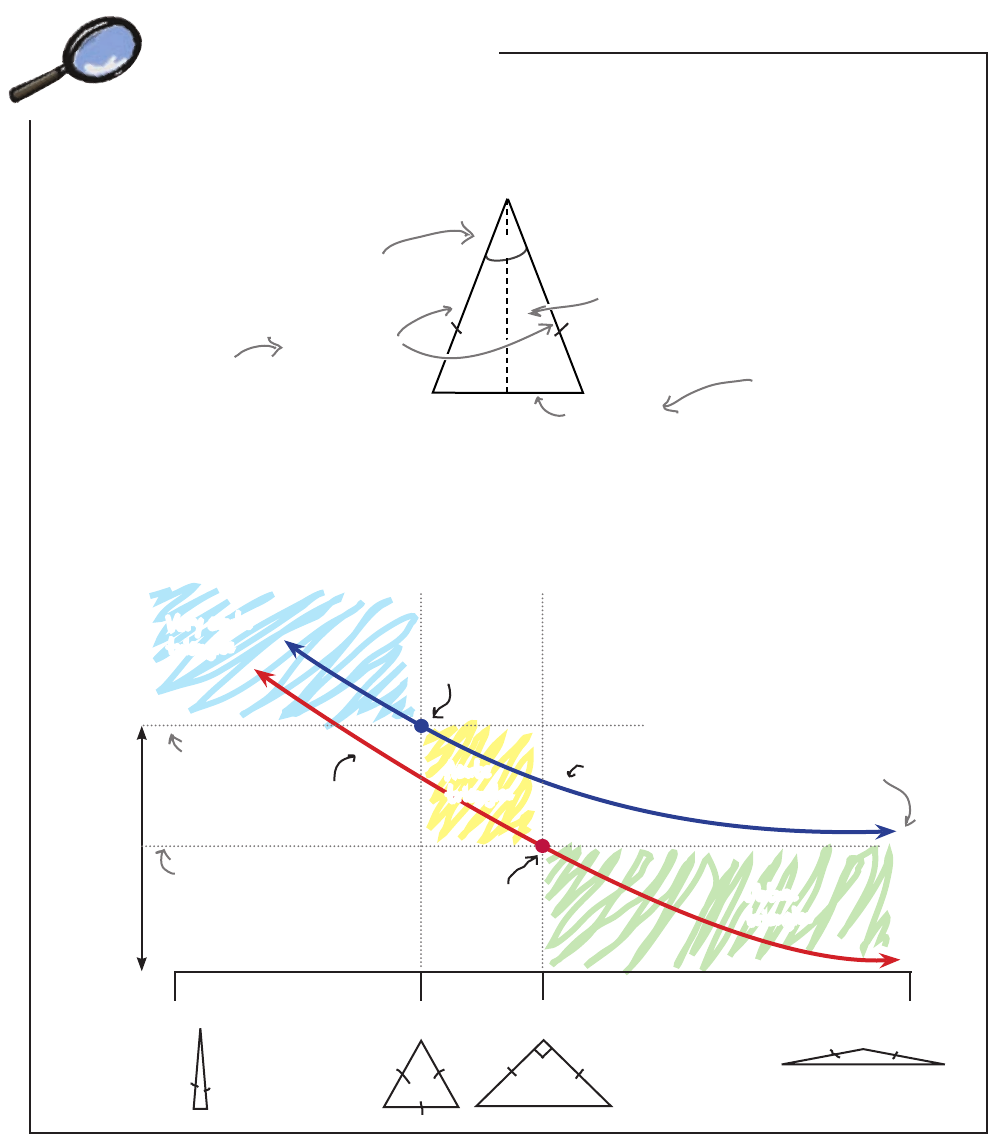
Side
Height
Base
0º
180º
60º 90º
V
ery acute
triangles
Obtuse
triangles
Acute
triangles
Equila
tera
l
triangle
Right
triangle
Base
1/2 base
Plot sides and height against base to find which zone
your apex angle is in: obtuse, acute, or very acute.
you are here 4 179
$1000!
the festival is almost ready
$2000
Budget
T
ickets
$15,000
Fencing –$3,750
Speakers –$2,000
NET
$9,250
ROCK FESTIVAL
TO-DO LIST
1) Fi
nd a venue
2) Sor
t out secur
i
ty fenci
ng
3) Sound system!!
4) Dr
inks/me
rc
h s
t
and?
Grea
t choic
e ther
e—
y
ou sav
ed y
ourself
Q:
Are you sure it’s OK to be
estimating angles like this? Don’t we
always need to work out exactly what
the angle is?
A:If the problem or question requires
a precise answer along the lines of “what
is angle x,” then you’ll need to find the
angle exactly, but sometimes it’s possible
to solve a problem just by knowing roughly
what an angle is. For example, is it a right
angle? Or maybe just is it acute or obtuse?
Q:
And this is isosceles only, yeah?
A:Yes, this technique only works
reliably for an isoceles triangle—where
two angles and two sides are the same. An
equilateral triangle is an isoceles triangle
with an extra matching side, so it works
for those, too, but then they’re pretty easy
to spot.
Q:
What if I only know the base and
the side, or the base and the height?
A:Sometimes that’s all you need. Any
time the base is greater than twice the
height you know you’ve got an angle more
than 90º.You really only need both for that
tricky zone between 60º and 90º.
But don’t worry—if you’ve got two out of
three for the base, side, and height lengths,
you can use the good old Pythagorean
Theorem to find the other. (This only works
for right and isoceles triangles—don’t
try it on a scalene triangle or you’ll come
unglued.)
Q:
OK—but how do I remember this?
I’m bound to get mixed up about the
base and sides and and which is greater
and less than which! I’m not a computer
you know.…
A:It’s almost certainly easier to
remember the zones on the graph than it is
to remember the inequalities.
So, sketch that graph, mark what you know
about the 60º and 90º triangles on it, and
label the zones.
Q:
Really? You think I could draw it
just like that?
A:Go on…give it a shot on a scrap of
paper now. It’s a really time efficient way to
check your answers in an exam by the way.
180 Chapter 4
Get Head First 2D Geometry now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

