Hughes/Computer Graphics, 3/E

Chapter 11. Transformations in Three Dimensions

11.1. Introduction

Transformations in 3-space are in many ways analogous to those in 2-space.

• Translations can be incorporated by treating three-dimensional space as the subset E³ defined by w = 1 in the four-dimensional space of points (x, y, z, w). A linear transformation whose matrix has the form 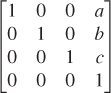, when restricted to E³, acts as a translation by [a b c]^T on E³.

• If T is any continuous transformation that takes lines to lines, and O denotes the origin of 3-space, then we can define

and the result ...