Illuminating Statistical Analysis Using Scenarios and Simulations

56For Part I

(A)   Figure 56.1 is a histogram showing the results of 1000 repetitions of flipping a fair coin 100 times. The results are the number of times the 100 flips came up with various proportions of heads. Does this look approximately like a normal distribution? Eyeballing this histogram, what is the approximate 95% confidence interval for a fair coin? What is the approximate 99% confidence interval?

Figure 56.1

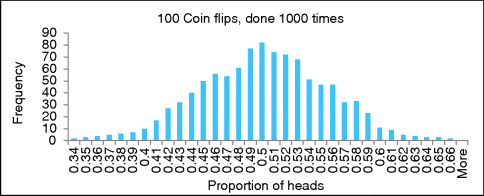
Answer: Yes, it approximates a normal distribution. It looks like about 950 of the 1000 proportions (95%) are in the interval 0.4–0.6. About 50 (5%) of the results have proportions outside this interval, with about 25 (2.5%) on each side (in each tail). Also, although it is hard to eyeball, about 990 of the 1000 proportions (99%) are betwen about 0.37 and about 0.63 inclusive, with about 5 (0.5%) in each tail outside this interval. (Simulating 10,000 repetitions would be better.)

(B)   Looking at Table 56.1, check whether your eyeballed 95% confidence interval matches the theoretical results one should obtain when flipping fair coins 100 times. (Recall that the margin of error is the half-width of the 95% confidence interval and can be expressed as a percentage rather than a proportion.)

Table 56.1

Sample size	100	500	1000	1500
Margin of error (%)	±9.80	±4.38	±3.10	±2.53

Answer: Yes, it does. 50% ± 9.8% is about 40–60%, or 0.4–0.6 proportions.

(C) ...