Illuminating Statistical Analysis Using Scenarios and Simulations

57For Part II

(A)   Figure 57.1 is a simulation histogram of 1000 sample means. The samples come from a population with an unknown mean and variance. Does this look approximately like a normal distribution? What is your best rough estimate for the population mean?

Figure 57.1

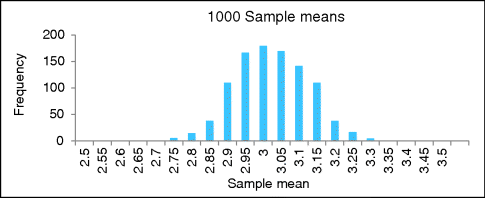
Answer: Yes, it approximates a normal distribution. The unknown population mean is most likely close to 3.

(B)   What interval holds about 95% of the results?

Answer: Between about 2.8 and 3.2. About 25 of the sample means are less than or equal to 2.8, and about 25 are greater than 3.2. (Remember that with a histogram, each bar is the count of the sample means that are less than or equal to (≤) the number label for the bar itself and strictly greater than (>) the number label for the bar to the left.)

(C)   So what does the standard error equal, approximately?

Answer: Since about two (1.96 rounded) standard errors on each side of 3 will hold 95% of the sample means (since it approximates a normal distribution), and the interval is about 3.0 ± 0.2, the standard error should equal about .

(D)   Figure 57.2 is a simulation histogram of 1000 sample mean differences. What is your best estimate for the difference between the actual population means?

Figure 57.2

Answer: About 0.5

(E)   What interval holds ...