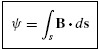4
THE CONCEPT OF “LOOP” INDUCTANCE
In this chapter we examine the calculation of the “loop” inductance of various configurations of closed current loops.
4.1 SELF INDUCTANCE OF A CURRENT LOOP FROM FARADAY’S LAW OF INDUCTION
Faraday’s law of induction, discussed in Chapter 3, is fundamental to the notion of inductance. For example, consider the circular loop of conducting wire shown in Fig. 4.1. Suppose that we cut a small gap in the loop and inject a current I into that gap so that the current flows around the loop in the counterclockwise direction as shown in Fig. 4.1. This current will, by the right-hand rule, produce a magnetic flux density B threading the surface s that the current surrounds. We have shown this surface as being flat to simplify the discussion, although any surface shape will give the same result as long as it is surrounded by the loop. For a current directed in the counterclockwise direction around the loop, the magnetic field is directed upward through the surface surrounded by the loop. The total magnetic flux penetrating the loop is obtained as
FIGURE 4.1. Loop inductance by Faraday’s law.
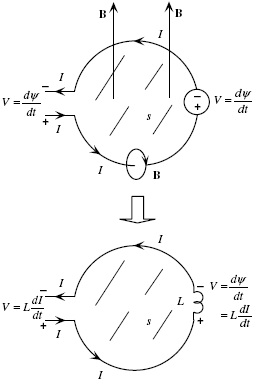
where s is the surface the current loop surrounds. If the current and associated magnetic field varies with time, Faraday’s law of induction essentially provides ...