October 2012
Beginner
420 pages
9h 37m
English
book
Industrial Statistics with Minitab
by Pere Grima Cintas, Lluis Marco Almagro, Xavier Tort-Martorell Llabres
Content preview from Industrial Statistics with Minitab
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
8.6 Equivalence between Sigmas of the Process and Defects per Million Parts Using ‘Cumulative Probability’
A process is said to be ‘Six Sigma’ when the distance between the nominal value and the tolerance limits of the produced output is equal to six times the standard deviation with which the output is produced. Likewise, a process is ‘Five Sigma’ if the tolerance limits are at five standard deviations, etc.
A Six Sigma process would look as follows:
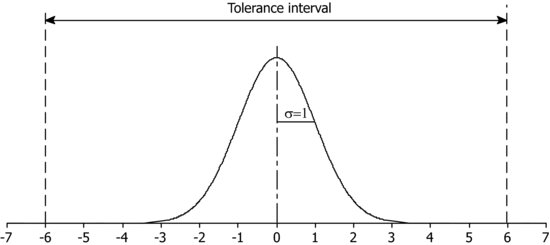
Knowing that the process will not always remain centred on its nominal value, it is assumed that the process is decentred 1.5 standard deviations to compute the proportion of defects that are produced. That is:
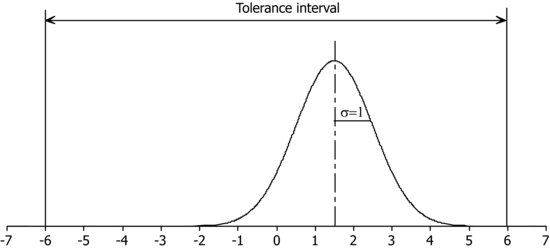
To compute the proportion of defects in relation to the sigmas of the process, set σ=1 and vary the tolerance values. Tolerances ±6 correspond to a 6σ process, ±5 to a 5σ process, etc.
The default number of decimal points has been changed in columns C3 to C6: Highlight the columns. Editor > Format Column > Numeric …
Column C6 contains the proportion of defects. To convert to ppm multiply these values by 1000000. For example, a process 3.5σ produces 22750 ppm.
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.