October 2012
Beginner
420 pages
9h 37m
English
book
Industrial Statistics with Minitab
by Pere Grima Cintas, Lluis Marco Almagro, Xavier Tort-Martorell Llabres
Content preview from Industrial Statistics with Minitab
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
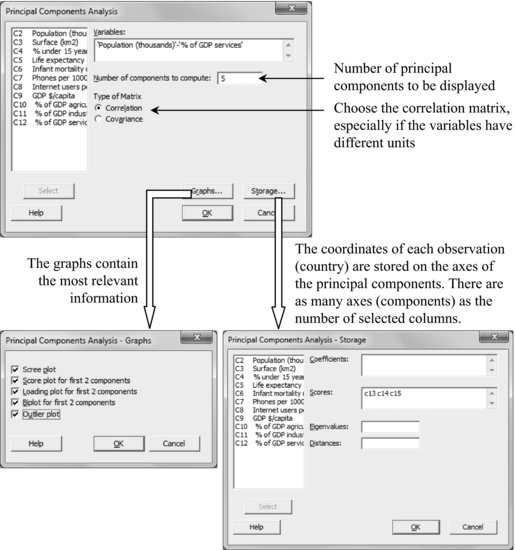
24.2 Principal Components
Statistical method used to compute new variables function of the original ones. These new variables are called ‘principal components’ and it is expected that few of them contain most of the information in the data.
Stat > Multivariate > Principal Components
In case the covariance matrix is chosen, the sum of the eigenvalues is equal to the sum of the variables’ variances. In case the correlation matrix is chosen, the data will be normalized and the sum of the eigenvalues will be equal to the number of variables. In either case, the eigenvalues represent each component's contribution to the explanation of the variability of the data.
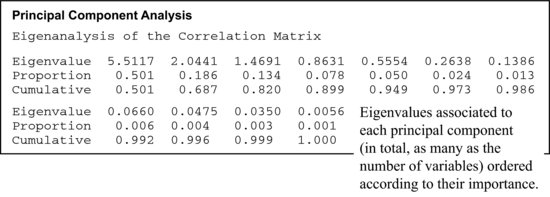
The first part on the shown output list provides information on the magnitude of the eigenvalues, ordered from highest to lowest, on the proportion they represent with respect to the total (proportion of the global variability explained by this component), and on the cumulative proportion.
Eigenvalues:
5.5117 + 2.0441 + 1.4691 + 0.8631 + 0.5554 + 0.2638 + 0.1386 + 0.0660 + 0.0475 + 0.0350 + 0.0056 = 11
50.1% + 18.6% ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.