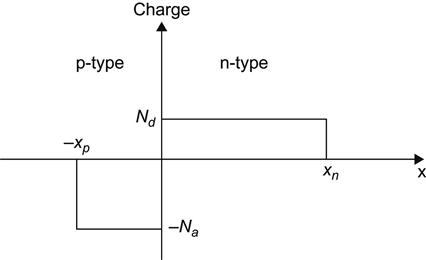
In our case assuming:
(1.234)
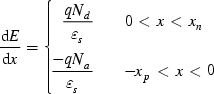 (1.234)
(1.234)then
(1.235)
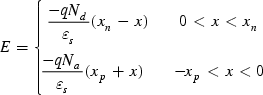 (1.235)
(1.235)The electric field is continuous and it also equals zero outside the junction region, thus:
(1.236)
which yields: ...
Get Integrated Nanophotonic Devices, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

