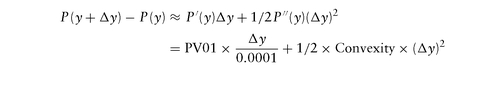Interest Rate Swaps and Their Derivatives: A Practitioner's Guide

APPENDIX A

Taylor Series Expansion

In this appendix, we review the Taylor Series expansion formula from ordinary analysis. This expansion is commonly used to relate sensitivities (risk, PV01, convexity) to profit and loss (P&L) for financial instruments (bonds, swaps, . . . ), as shown in Chapters 1 and 6. The much-dreaded Ito′s Lemma used in Chapters 10 and 11 is basically Taylor Series expansion in a stochastic setting, and can be easily used in practice via a multiplication table.

FUNCTION OF ONE VARIABLE

For a function of one variable, f (x), the Taylor Series formula is:

f (x + Δx) = f (x) + f ^′(x)Δx + 1/2 f ^′′(x)(Δx)² + . . . + 1/n! f ⁽ⁿ⁾(x)(Δx)ⁿ + . . . .

where f ^′(x) is the first derivative, f ^′′(x) the second derivative, f ⁽ⁿ⁾ (x) the n-th derivative, and so on. In practice, we usually just use the first two derivatives, and ignore the effect of the remaining higher-order terms:

f (x + Δx) - f (x) = f ^′(x)Δx + 1/2 f ^′′(x)(Δx)² + Higher Order Terms

For example, considering the Price-Yield formula for bonds, we have:

FUNCTION OF SEVERAL VARIABLES

A similar formula holds for functions of several variables f (x₁ , . . . , x_n). This is usually written as

For example, using Black′s Formula, the expected P&L of an option is usually computed by considering the first-order ...