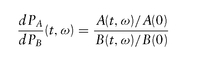Interest Rate Swaps and Their Derivatives: A Practitioner's Guide

APPENDIX C

Girsanov′s Theorem and Change of Numeraire

The change of numeraire formula in Chapter 11 relates the risk-neutral probability sets when switching numeraires via their likelihood ratios (Radon-Nikodym derivative):

When working with diffusions, Girsanov′s Theorem uses the same likelihood ratios to relate Brownian motions under one probability to another. We will use the following version of it.¹

 

Girsanov′s Theorem

 

Let B₁(t, ω) be a Brownian motion under a probability measure P₁: B₁(t, ω) ~ N(0, t) under P₁. Define a new probability measure P₂ related to P₁ through their likelihood ratios as follows:

for a random process γ (s, ω). Then subject to some regularity conditions on γ (s, ω), the process B₂(t, ω) defined as

(or dB₂(t, ω) = dB₁(t, ω) + γ (t, ω)dt in differential format) is a Brownian motion under P₂: B₂(t, ω) ~ N(0, t) under P₂.

CONTINUOUS-TIME, INSTANTANEOUS-FORWARDS HJM FRAMEWORK

As for short-rate models, the original HJM formulation of their framework was in continuous time and in terms of instantaneous forward rates, related to discount factors as follows:

We assume the following general dynamics for the 1-factor (can easily be generalized to multifactor) ...