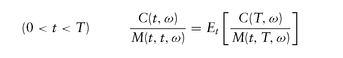Interest Rate Swaps and Their Derivatives: A Practitioner's Guide

CHAPTER 11

Forward-Measure Lens

We have so far focused on risk-neutral valuation using the intuitive ″money-market″ numeraire. In this framework, the main pricing operator is

which we have interpreted as the expected value of terminal option payoff, when stochastically discounted back to valuation date. Written another way,

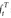
where M(t, T, ω) =is the value of a money-market account with initial unit deposit at time t, and continually rolled over until T along the series of instantaneous short rates r(u, ω). Since M(t, t, ω) = 1, the above two formulae are equivalent. However, the second formula highlights the required martingale property: It states that having chosen the money-market account as the currency (numeraire), then all relative prices in the future should have 0 expected P&L. This requirement pins down the risk-neutral probabilities used when taking expected values.

NUMERAIRES ARE ARBITRARY

Derivatives prices being relative prices, it turns out that a more general result holds, stating that no matter what the chosen currency/numeraire, then relative prices of all assets (underlyings and derivatives) with respect to that numeraire should have 0 expected P&L, that is, relative ...