Intermarket Trading Strategies

3

Regression

Man loves company, even if only that of a small burning candle.

-Georg Christoph Lichtenberg

 

Regression involves the use of the concept of correlation in predicting future values of one security (dependent variable), in terms of another (independent or predictor variable). For example, if there is high correlation between the S&P 500 and the Euro Stoxx 50 index we can use the linear regression equation to predict future values of the S&P by extending the least squares or linear regression line into the future.

The mere fact that we use our knowledge of the relationship between the two indices to predict values of the S&P 500 from the Euro Stoxx doesn’t imply that changes in the Euro Stoxx cause changes in the S&P. These could be caused by a number of economic or geopolitical reasons which affect both indices.

3.1 THE REGRESSION EQUATION

The general form of a simple linear regression is: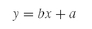

(3.1)

where a (regression constant) is the intercept and b (regression coefficient) is the slope of the line, y is the dependent variable and x is the independent variable. Estimates for the values of a and b can be derived by the method of ordinary least squares. The method is called “least squares” because estimates of a and b minimize the sum of squared error estimates for the given data set. The regression constant a and the coefficient b are calculated using the following formulae: ...