Introduction to Combinatorics, 2nd Edition

EXERCISE SOLUTIONS

SOLUTIONS FOR CHAPTER 1

1.5 There are 2⁹⁹ binary strings of length 99. Half of these, 2⁹⁸, have an odd number of 1′s. The reason is that, regardless of the first 98 bits, the last bit may be chosen to make the total number of 1′s even or odd.

1.7 There are nⁿ such functions.

1.17 There are 2ⁿ² different binary relations on an n-set.

1.20 Since the tenth row of Pascal’s triangle is 1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1, we have (a + b)¹⁰ = a¹⁰ + 10a⁹b + 45a⁸b² + 120a⁷b³+210a⁶b⁴ + 252a⁵b⁵ + 210a⁴b⁶ + 120a³b⁷ + 45a²b⁸ + 10ab⁹ + b¹⁰.

1.21 By the binomial theorem, the coefficient is = 184,756.

1.25 By the multinomial theorem, (a + b + c)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴ + 4a³c 12a²bc + 12ab²c + 4b³c + 6a²c² + 12abc² + 6b²c² + 4ac³ + 4bc³ + c⁴.

1.26 By the multinomial theorem, the coefficient is = 22,170,720.

1.27 By simplifying, we see that

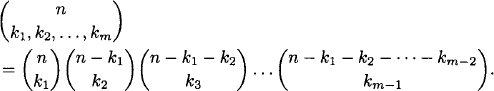
1.30 (a) The number of paths is = 3,268,760.

(b) The number of paths is = 10,361,546,974,682,663,760.

1.32 The identity to ...