CHAPTER 2
GENERATING FUNCTIONS
Generating functions are algebraic objects that provide a powerful tool for analyzing recurrence relations. In this chapter, we will cover the basic theory of generating functions and examine many specific examples.
2.1 Rational generating functions
Given any sequence a0, a1, a2,…,the ordinary generating function is
(2.1) 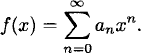
The generating function f(x) contains all of the information about the sequence {an}, and, being an algebraic entity, it is often easier to manipulate than the sequence itself. The term an is recovered by finding the coefficient of xn in f(x).
 EXAMPLE 2.1 Generating function for the Fibonacci sequence
EXAMPLE 2.1 Generating function for the Fibonacci sequence
Find the ordinary generating function for the Fibonacci sequence {F0, F1, F2,…}.
Solution: Let ![]() . We obtain
. We obtain
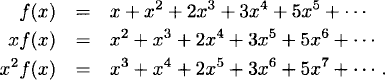
Through mass cancellation, the recurrence relation for the Fibonacci numbers yields
![]()
and
(2.2) ![]()
The function f(x) contains complete ...
Get Introduction to Combinatorics, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

