CHAPTER 3
THE PIGEONHOLE PRINCIPLE
The pigeonhole principle is an important key to solving many problems in combinatorics. In this chapter, we discuss several versions of the pigeonhole principle and give many applications.
3.1 The principle
The most important theorem in existential combinatorics is also the simplest: the pigeonhole principle. It occurs in many variations, a few of which we discuss here, and says that not every element in a set is below average and not every element is above average. We now state and prove a general version.
Pigeonhole principle. If f : A → B is a function, with A and B finite nonempty sets, then the following two statements hold:
Proof. We prove (1) by contradiction. Suppose that |f−1 (b)| < |A|/|B| for all b ![]() B. Then
B. Then
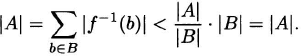
We conclude that |A| < |A|, an absurdity. Therefore, our assumption that |f−1 (b)| < |A|/|B| for all b ![]() B is false. Hence, there exists ...
B is false. Hence, there exists ...
Get Introduction to Combinatorics, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

