Introduction to Cryptography with Coding Theory, 3rd Edition

B.12 Examples for Chapter 21

Example 40

All of the elliptic curves we work with in this chapter are elliptic curves mod $n\text{.}$ However, it is helpful use the graphs of elliptic curves with real numbers in order to visualize what is happening with the addition law, for example, even though such pictures do not exist mod $n\text{.}$

Let’s graph the elliptic curve $y^2=x(x-1)(x+1)\text{.}$ We’ll specify that $-1\le x\le 3$ and $-5\le y\le 5\text{,}$ and make sure that x and y are cleared of previous values.

> x:=’x’;y:=’y’;implicitplot($\mathrm{y}\stackrel{\mathbf{ˆ}}{\phantom{\mathbf{a}}}$2=x*(x-1)*(x+1), x=-1..3,y=-5..5)

B.12-1 Full Alternative Text

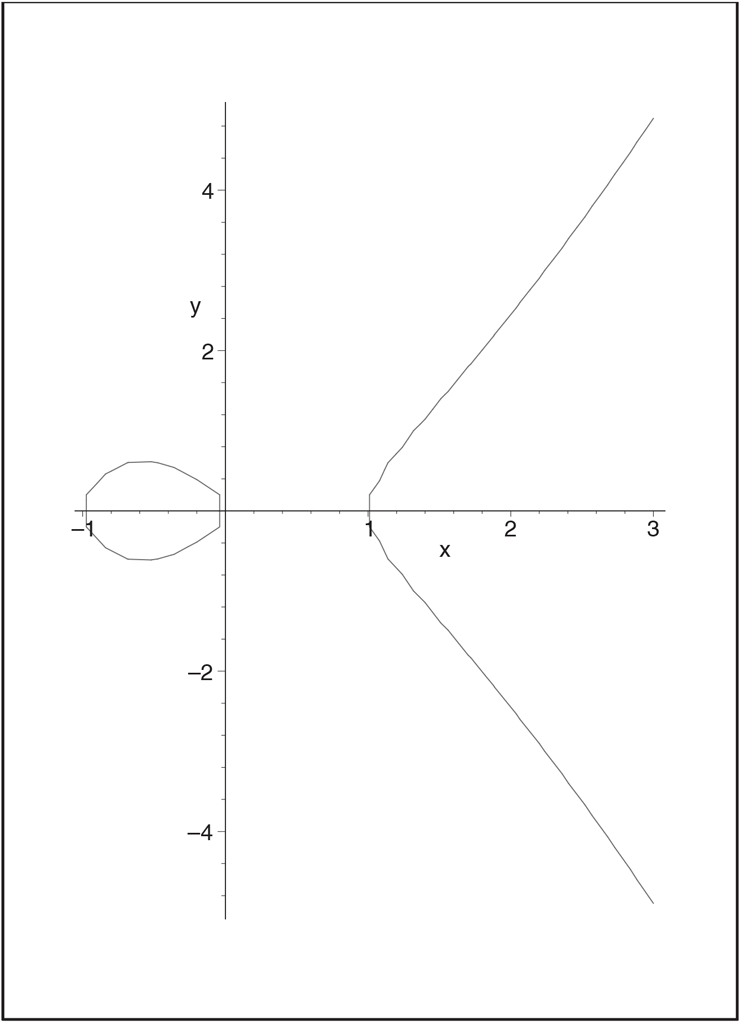
Example 41

Add the points (1, 3) and (3, 5) on the elliptic curve $y^2\equiv x^3+24x+13(\text{mod ...}$