Introduction to Digital Systems: Modeling, Synthesis, and Simulation Using VHDL

9.10 STATE OPTIMIZATION

In the finite-state machine examples we discussed in previous sections that the number of states wasvery small. It was very easy to determine the minimum number of states possible that describe the behavior of the finite-state machine without introducing unnecessary (redundant) states. However, as the number of states increases, it becomes difficult to distinguish between possible states. The initial design attempt may include more states than are required by a finite-state machine. Some of the states are redundant, which increases the complexity of the finite-state machine unnecessarily.

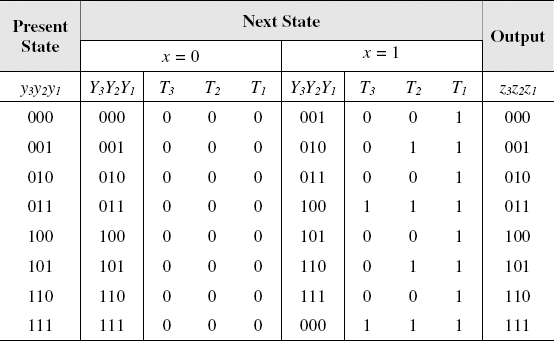
Figure 9.52 State Assigned Table of a 3-Bit Up Counter Using T Flip-Flops

State minimization is the process of finding and eliminating the redundant states, which are also referred to as equivalent states. Eliminating equivalent states will reduce the number of flip-flops and simplify the combinational logic of the finite-state machine. Two states are equivalent if and only if for all possible input sequences, the finite-state machine generates the same output regardless of whether it starts at one or the other state. It follows that the next states to two equivalent states must also be equivalent. Knowing all possible input and output sequences of a finite-state machine, one could automate the process by comparing two states at a time. Another less tedious method is to ...