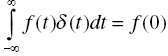2SIGNAL AND SYSTEMS
This chapter provides a mathematical foundation for the analysis of signals, noise, and linear signal systems that will be used in subsequent chapters. The reader who is familiar with these fundamental techniques may choose to move on to the next chapter.
2.1 SIGNAL ANALYSIS
2.1.1 Delta Function
The delta function was invented by a physician, P. A. M. Dirac, to mathematically describe the quantum mechanics [1]. Although the intuitive understanding is rather easy, its mathematical background differs from conventional functions [2]. Therefore, it is called distribution or hyperfunction. The mathematical treatment as hyperfunction is highly abstract and it is hard for engineers (who just apply the delta function to practical matters) to follow its treatment. In some engineering textbooks, the description on the Dirac delta function is not sufficient enough. In this book, we primitively describe the delta function as a (generalized) limit of conventional functions without touching the argument of hyperfunctions. The delta function plays an important role to develop theories of the Fourier analysis and to analyze signal and systems as described in this book.
2.1.1.1 Definition of the Delta Function
Delta function is defined through integral as follows:
where f(t) is an arbitrary function being continuous at . We consider a following function
Inserting ...
Get Introduction to Digital Mobile Communication, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.