Introduction to Finance: Markets, Investments, and Financial Management, Fourteenth Edition

Chapter LE9. LEARNING EXTENSION 9: Annuity Due Problems

FUTURE VALUE OF AN ANNUITY DUE

In contrast with an ordinary annuity, an annuity due exists when the equal periodic payments occur at the beginning of each period. Let's return to the example used in the "Future Value of an Annuity" section in this chapter. Recall that the problem involved a three-year annuity, $1,000 annual payments, and an 8 percent interest rate. However, let's assume that the first payment now is made at the beginning of the first year, namely at time zero. This will allow the first $1,000 payment to earn interest for three years, the second payment to earn interest for two years, and the third payment to earn interest for one year.

The calculation process to find the future value of this annuity due problem can be demonstrated as follows:

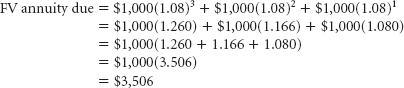
Notice that by making the first payment now the future value of this annuity at the end of three years will be $3,506. This contrasts with a future value of $3,246 if payments are delayed by one year, as would be the case with an ordinary annuity.

Table-based Solution:

Equation 9.6 can be easily modified to handle annuity due problems as follows:

where FVAD is the future value of an annuity due and the (1 + r) factor effectively compounds each payment by one more year to reflect ...