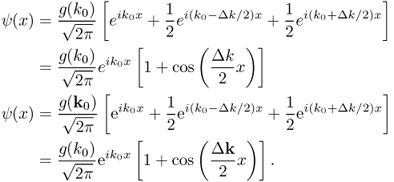Introduction to Nanomaterials and Devices

Appendix A

Derivation of Heisenberg Uncertainty Principle

Heisenberg uncertainty principles can be derived by different methods. This appendix uses the wave packet to derive the uncertainty principles. For the sake of simplicity, the case of the one-dimensional wave packet is presented here. Then the wave function only depends on x and t.

A.1

For t=0, we have

A.2

and

A.3

Thus, g(k) is the Fourier transform of ψ(r,0). The wave packet is given by x-dependent wave function expressed in Equation A.2. If |g(k)| has the shape depicted in Fig. A.1 and ψ(x), instead of having the form shown in Equation A.2, is composed of three plane waves with wave vectors of k0, k0 + Δk/2, and k0 − Δk/2 and amplitudes proportional to 1, , and , then one can write the new wave packet as

A.4

From Fig. A.1, |ψ(x)| is maximum at x = 0. This result is due to the fact that when x is zero, the three waves are in phase ...