Introduction to Nonlinear Aeroelasticity

6Discontinuous Nonlinearities

6.1 Introduction

Many nonlinearities that are encountered in engineering systems, including aeroelastic ones, are discontinuous in nature. The most ubiquitous example of such nonlinearities is friction that, in its simplest form, can be modelled as a constant force that changes sign when the velocity crosses zero. Several other such functions are common, especially in bearings and actuators. In this chapter we will concentrate on the latter and, in particular, on piecewise linear stiffness. Friction in moving surfaces of aeroelastic systems is, in general, an energy extraction mechanism and will most often suppress aeroelastic instabilities. On the other hand, piecewise linear stiffness in actuators is well‐known as causing important instabilities, including limit cycle and aperiodic oscillations.

A general form of a discontinuous nonlinear function f(x), where x is a state vector and f is a vector of functions, is given by

(6.1)

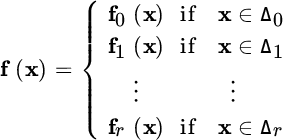
where f_i(x) are different linear or nonlinear functions and are sub‐regions of n‐dimensional space, separated by ...