Introduction to Numerical Electrostatics Using MATLAB

11 Probabilistic Potential Theory

11.1 Random Walks and the Diffusion Equation

Consider a grid with nodes (i, j) spaced one unit apart in both axes. These nodes, at this point, have nothing to do with electrostatics –– there are no voltages, charges, or fields present. Instead, there is a particle undergoing a random walk. Brownian motion,¹ for example, is a random walk of particles. Random walks have various defining characteristics; the random walk discussed here is defined as follows:

1. There is a particle sitting at one of the nodes. At time (m − 1) the probability of the particle being at node (i, j) is P_m−1(i, j).
2. Every second the particle will quickly jump to an adjacent node. Adjacent means to the left (−x), right (+x), up (+y) or down (−y). Diagonal jumps and multinode jumps are not allowed.
3. All of the jumps have equal probability; that is, the probability of any given jump is .

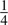Four examples of such a walk, reminiscent of a drunkard wandering through a parking lot, are shown in Figure 11.1. In each of these examples the particle started at (0,0).

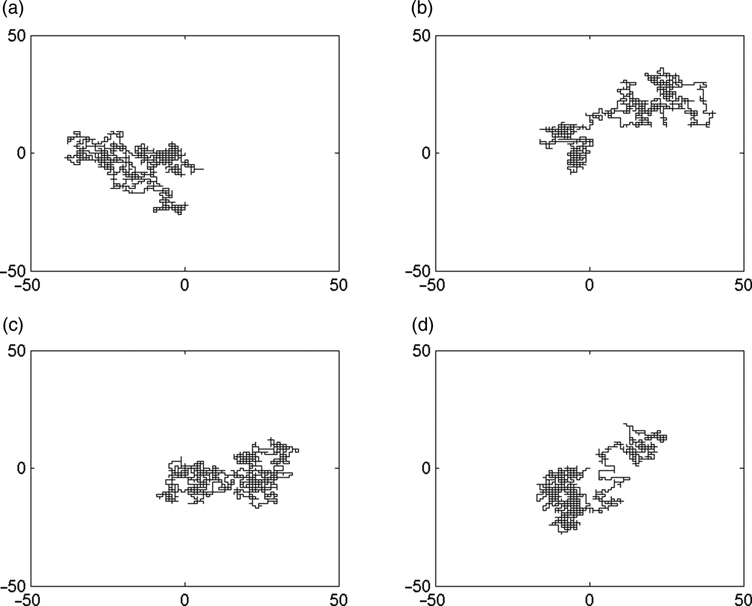
FIGURE 11.1 Four fixed-step two-dimensional random walks.

At a given time, a particle can arrive at node (i, j) only if it started from one of the (four) adjacent nodes. The probability of a particle arriving at ...