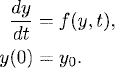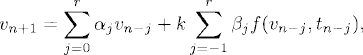CHAPTER 5
TWO-STEP AND MULTISTEP METHODS
The character of some equations, such as the equations of motion in a many-body problem in Newtonian mechanics, requires methods of high and very high orders of accuracy. The use of high-order one-step methods (such as Runge-Kutta methods) for such problems turns out to be computationally very expensive. For this reason multistep methods have been developed. These methods can be both of very high accuracy and fast. In this chapter we study the leapfrog method, which is the simplest of all, and Adams methods, which include both explicit and implicit methods. At the end we show a simple example of the predictor-corrector strategy for multistep methods.
5.1 Multistep methods
Consider the initial value problem
Thus far, we have approximated equation (5.1) by one-step methods (see Definition 2.9). They have the form
If we know vn, we can calculate vn+1. Another class of methods are the multistep methods.1
Definition 5.1 A multistep method to approximate equation (5.1) is of the form
where αj and βj are given constants and r ≥ 1. The method is said to be explicit if β−1 = 0 and implicit otherwise.
The constants αj and βj, which ...
Get Introduction to Numerical Methods for Time Dependent Differential Equations now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.