Introduction to Plasmas and Plasma Dynamics

Single Fluid Equations of Magnetofluid Mechanics

We will consider basic single fluid theory with the following variables: 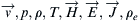v→,p,ρ,T,H→,E→,J→,ρe, a total of 16 unknowns. This set can be solved using the following equations with appropriate boundary conditions (Pai, 1962).

State:

p=ρRT=nkT.

Continuity:

∂ρ∂t+∇·(ρv→)=0.

Momentum:

ρ[∂v→∂t+(v→·∇)v→]=−∇p+∇·τ↔+ρeE→+J→×B→,where:τij=μ(∂ui∂xj+∂uj∂xi)−23μ(∇·v→)δij.

Energy:

ρDe¯mDt=−∇·(pv→)+∇·(v→·τ↔)+∇·Q→+J→·E→.

But note ...