Introduction to Probability and Stochastic Processes with Applications

CHAPTER 4

SOME CONTINUOUS DISTRIBUTIONS

In this chapter we will study some of the absolute continuous-type distributions most frequently used.

4.1   UNIFORM DISTRIBUTION

Suppose that a school bus arrives always at a certain bus stop between 6 AM and 6:10 AM and that the probability that the bus arrives in any of the time subintervals, in the interval [0,10], is proportional to the length of the subinterval. This means it is equally probable that the bus arrives between 6:00 AM and 6:02 AM as it is that it arrives between 6:07 AM and 6:09 AM. Let X be the time, measured in minutes, that a student must wait in the bus stop if he or she arrived exactly at 6:00 AM. If throughout several mornings the time of the bus arrival is measured carefully, with the data obtained, it is possible to construct a histogram of relative frequencies. From the previous description it can be noticed that the relative frequencies observed of X between 6:00 and 6:02 AM and between 6:07 and 6:09 AM are practically the same. The variable X is an example of a random variable with uniform distribution. More precisely it can be defined in the following way:

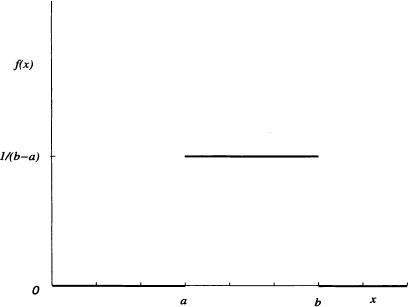
Figure 4.1   Density function of a uniform distribution

Definition 4.1 (Uniform Distribution) It is said that a random variable X is uniformly distributed over the interval [a, b], with a < b real numbers, if its density function is given by:

The probability ...