CHAPTER 5
RANDOM VECTORS
In the previous chapters, we have been concentrating on a random variable defined in an experiment, e.g., the number of heads obtained when three coins are tossed. In other words, we have been discussing the random variables but one at a time. In this chapter, we learn how to treat two random variables, of both the discrete as well as the continuous types, simultaneously in order to understand the interdependence between them. For instance, in a telephone exchange, the time of a call arrival X and a call duration Y or the shock arrivals X and the consequent damage Y are of interest. One of the questions which also comes to mind is, can we relate two random variables defined on the same sample space, or in other words, can two random variables of the same spaces be correlated? Some of these questions will be discussed and answered in this chapter.
5.1 JOINT DISTRIBUTION OF RANDOM VARIABLES
In many cases it is necessary to consider the joint behavior of two or more random variables. Suppose, for example, that a fair coin is flipped three consecutive times and we wish to analyze the joint behavior of the random variables X and Y defined as follows:
X := “Number of heads obtained in the first two flips”.
Y := “Number of heads obtained in the last two flips”.
Clearly:
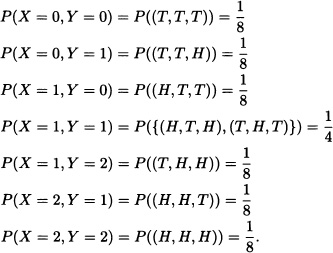
This information can be summarized in the following table:
Definition 5.1 (n-Dimensional ...
Get Introduction to Probability and Stochastic Processes with Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

