Introduction to Stochastic Analysis: Integrals and Differential Equations

Chapter 5

Itô’s Formula

 

 

For finite-variation continuous processes X and functions F ∈ C¹(), recall the main formula of integration¹

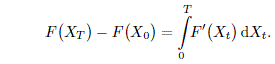
From example 4.10 we see that it does not hold for stochastic integrals. Its stochastic counterpart is the Itô formula which is proved below. For this, we need the Taylor² formula with the remainder in some special Peano-type³ form.

LEMMA 5.1 (Taylor formula).– Let F ∈ C²() have a uniformly continuous second derivative (for example, F has a bounded third derivative F'"). Then

where, the remainder term satisfies the estimate |R(x, y)| r(|y − x|)(y − x)² with an increasing function r: → such that lim_h↓0r(h) = 0.

Proof. We use the Taylor formula with the well-known Lagrange remainder term

where the point ξ = ξ(x, y) is between x and y (x < ξ < y or y < ξ < ...