Introduction to the Variational Formulation in Mechanics

8Torsion of Bars

8.1 Introduction

In this chapter the mechanical theory for the modeling of torsion of regular prismatic bars under the kinematical hypotheses of Saint‐Venant is presented. The variational framework developed in Chapter 3 is manipulated to achieve this goal. We will see in detail the construction of kinematically admissible sets and spaces of motion actions, and the strain (rate) operator will be defined. From this Saint‐Venant kinematical model, compatible internal stresses and external forces are then characterized by mathematical duality and, through the concept of mechanical equilibrium and compatibility provided, respectively, by the Principle of Virtual Power (PVP) and by the Principle of Complementary Virtual Power (PCVP) the variational formulations will be exposed regardless of the material behavior. Then, as an illustrative example, the case of elastic materials within the range of infinitesimal strains is addressed.

8.2 Kinematics

The kinematical model is governed by the so‐called Saint‐Venant kinematical hypotheses (see Figure 8.1), which are the following

• regular prismatic bars (equally called bars) are considered, that is, the transversal section, denoted by 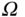, with a smooth delimiting boundary 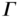, is constant along the longitudinal bar axis, of length ...