Introductory Mathematics for Engineering Applications

Quadratic Equations in Engineering

CHAPTER 2

In this chapter, the applications of quadratic equations in engineering are introduced. It is assumed that students are familiar with this topic from their high school algebra course. A quadratic equation is a second-order polynomial equation in one variable that occurs in many areas of engineering. For example, the height of a ball thrown in the air can be represented by a quadratic equation. In this chapter, the solution of quadratic equations will be obtained by three methods: factoring, the quadratic formula, and completing the square.

2.1 A PROJECTILE IN A VERTICAL PLANE

Suppose a ball thrown upward from the ground with an initial velocity of 96 ft/s reaches a height h(t) after time t s as shown in Fig. 2.1. The height is expressed by the quadratic equation h(t) = 96 t − 16 t² ft. Find the time t in seconds when h(t) = 80 ft.

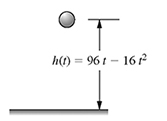
Figure 2.1 A ball thrown upward to a height of h(t).

Solution:

h(t) = 96 t − 16 t² = 80

or

Equation (2.1) is a quadratic equation of the form ax² + bx + c = 0 and will be solved using three different methods.

Method 1: Factoring Dividing equation (2.1) by 16 yields

Equation (2.2) can be factored as

(