Introductory Statistics and Analytics: A Resampling Perspective

11

REGRESSION

With correlation, all we can measure is the relative strength of an association and whether it is statistically significant. With regression, we can model that association in a linear form and predict values of Y given the values of X.

After completing this chapter, you will be able to

• specify the equation format for a simple linear regression model,
• define residuals (errors),
• fit a linear regression line by eye,
• describe how fitting the regression line by minimizing residuals works,
• use the fitted regression model to make predictions of y, based on the values of x,
• interpret residual plots,
• determine the confidence interval for the slope of a regression line.

The simple form of a linear regression model is as follows:

y = ax + b

We read this as “y equals a times x, plus a constant b.” You will note that this is the equation for a line with slope a and intercept b. The value a is also termed the coefficient for x (Figure 11.1). The constant b is where the regression line intersects the y-axis and is also called the y-intercept.

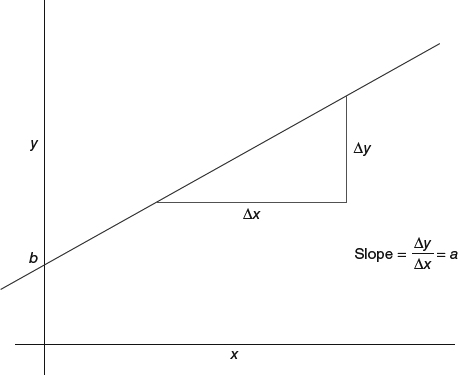
Figure 11.1 Slope and intercept of a line.

11.1 FINDING THE REGRESSION LINE BY EYE

Using the baseball payroll example and assuming that a correlation exists between the payroll amount in dollars and the number of wins over three seasons, can we predict wins based on a given payroll amount?

On the basis of Figure 11.2, it appears that an ...