Linear Algebra

5

Linear Operators

5.1 INTRODUCTION

The advantage of representing a linear operator on a finite-dimensional vector space by a matrix lies in the freedom to choose suitable bases of the vector space. An appropriate basis will result in a relatively simple matrix of the linear operator which will enable us to understand the operator better. Ideally, one would like such a matrix to be as simple as a diagonal one such as

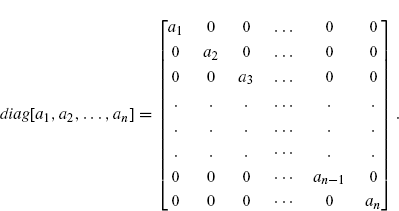
If a linear operator T on an n-dimensional vector space V can be represented by such a diagonal matrix, then just by counting the number of non-zero entries along the diagonal, one would know the rank as well as the nullity of ...