Chapter 1Understanding Propositional Logic
Propositional logic is about reasoning with propositions. These are sentences that can be assigned a truth value: true or false. They are built from primitive statements, called atomic propositions, by using propositional logical connectives. The truth values propagate over all propositions through truth tables for the propositional connectives. In this chapter I explain how to understand propositions and compute their truth values, and how to reason using schemes of propositions called propositional formulae. I will formally capture the concept of logically correct propositional reasoning by means of the fundamental notion of propositional logical consequence.
1.1 Propositions and logical connectives: truth tables and tautologies
1.1.1 Propositions
The basic concept of propositional logic is proposition. A proposition is a sentence that can be assigned a unique truth value: true or false.
Some simple examples of propositions include:
- The Sun is hot.
- The Earth is made of cheese.
- 2 plus 2 equals 22.
- The 1000th decimal digit of the number
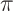 is 9.
is 9.
(You probably don't know whether the latter is true or false, but it is surely either true or false.)
The following are not propositions (why?):
- Are you bored?
- Please, don't go away!
- She loves me.
- is an integer.
- This sentence is false.
Here is why. The first sentence above is a question, ...
Get Logic as a Tool now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

