Logic for Computer Science and Artificial Intelligence

Chapter 4

First-order Terms

4.1. Matching and unification

4.1.1. A motivation for searching for a matching algorithm

Imagine that in example 3.9, you are given the first step of an alleged proof:

1)

without any justification, and that you (legitimately) wonder: “how can I be sure that this wff is a possible first step of a proof?”.

If formulas (structured strings) are represented as trees, answering this question reduces to finding what replacements should be carried out in the axiom schemas so as to find the desired wff (in a proof, this is the only possibility for the first step). We therefore try the axiom schemas one by one.

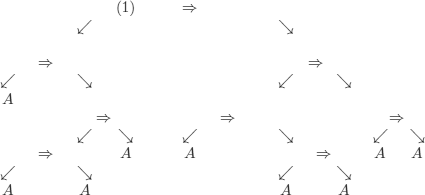
We will use X, Y, and Z for the meta-variables that appear in the axiom schemas to better emphasize that they are to be replaced.

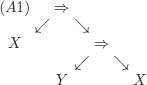
It is simple to see that there is no way to replace the variables in (A1) to identify (A1) with (1): we would need to replace X with A (rightmost leaf) and X with A ((A A) A) (leftmost leaf).

Let us try with (A2):

We realize ...