Loss Models: From Data to Decisions, 4th Edition

8.5 Coinsurance, deductibles, and limits

The final common coverage modification is coinsurance. In this case the insurance company pays a proportion, α, of the loss and the policyholder pays the remaining fraction. If coinsurance is the only modification, this changes the loss variable X to the payment variable, Y = αX. The effect of multiplication has already been covered. When all four items covered in this chapter are present (ordinary deductible, limit, coinsurance, and inflation), we create the following per-loss random variable:

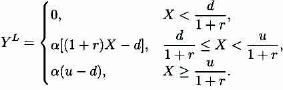
For this definition, the quantities are applied in a particular order. In particular, the coinsurance is applied last. For the illustrated contract, the policy limit is α(u − d), the maximum amount payable. In this definition, u is the loss above which no additional benefits are paid and is called the maximum covered loss. For the per-payment variable, Y^P is undefined for X < d/(1 + r).

Previous results can be combined to produce the following theorem, given without proof.

Theorem 8.7 For the per-loss variable,

The expected value of the per-payment variable is obtained as

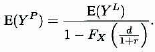
Higher moments are more difficult. Theorem 8.8 gives the formula for the second ...