Loss Models: From Data to Decisions, 4th Edition

14.4 The (a, b,1) class

Estimation of the parameters for the (a, b,1) class follows the same general principles used in connection with the (a, b, 0) class.

Assuming that the data are in the same form as the previous examples, the likelihood is, using (6.7),

The loglikelihood is

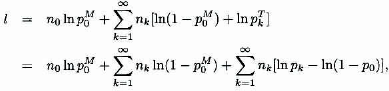
where the last statement follows from . The three parameters of the (a, b, 1) class are p^M₀, a, and b, where a and b determine p₁, p₂, ….

Then it can be seen that

with

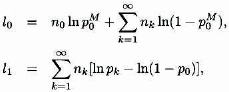
where l₀ depends only on the parameter p^M₀ and l₁ is independent of p^M₀, depending only on a and b. This separation simplifies the maximization because

resulting in

the proportion of observations at zero. This is the natural estimator because p^M₀ represents the probability of an observation of zero.

Similarly, because the likelihood factors conveniently, ...