3.3. Integer Discrete Cosine Transform–Based Schemes
3.3.1. Integer Discrete Cosine Transform
3.3.1.1. One-Dimensional Integer Discrete Cosine Transform and Its Fast Algorithm
Let x(n) (n = 0, 1, …, N−1) be a real input sequence. We assume that N = 2t, where t > 0. The scaled DCT of x(n) is defined as follows:
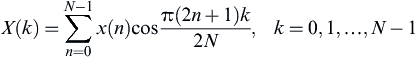 (3.10)
(3.10)
Let CN be the transform matrix of the DCT, that is
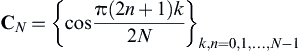 (3.11)
(3.11)
To derive the fast algorithm, we first get a factorization of the transform matrix based on the following lemma ...
Get Lossless Information Hiding in Images now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

