Machine Learning and Big Data with kdb+/q

CHAPTER 13Linear Regression

In this chapter, we introduce the notion of linear regressions and implement it within q. The linear regression model should be a starting point for nearly any problem where we want to establish a relationship between factors on one side and a dependent variable on the other side. The linear regression is in nature close to understanding the correlation between variables. Why do we start with linear models which model the linear response of the system? The straightforward answer in the spirit of the famous physicist and Nobel prize winner Richard Feynman is “because we can solve them”.

Linear regression corresponds to the modelling of a function based on the first‐order Taylor expansion in the vicinity of a point :

(13.1)

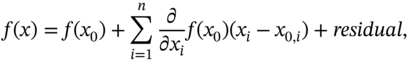
which can be ultimately recast into a linear model

(13.2)

where

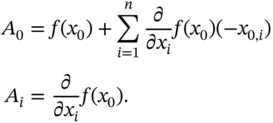
In physics, making a linear approximation is a suitable tool to start to explore a new physical problem or to explain an observed phenomenon. Since we have mentioned Richard Feynman, see Veltman et al. (1994) for instance, famous Feynman diagrams for describing the interaction ...