Machine Learning

5.13.3 Convergence and Steady-State Performance: Some Highlights

In this subsection, we will summarize some findings concerning the performance analysis of the DiLMS. We will not give proofs. The proofs follow similar lines as for the standard LMS, with a slightly more involved algebra. The interested reader can obtain proofs by looking at the original papers as well as in [84].

• The gradient descent scheme in (5.90), (5.91) is guaranteed to converge, meaning

${\mathit{\theta }}_k^{(i)}\underset{i\to \infty }{\overset{}{\to }}{\mathit{\theta }}_{*},$

provided that

${\mu }_k\le \frac{2}{{\lambda }_{max}\{{\Sigma }_k^{loc}\}},$

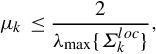
where

$\begin{array}{l}\hfill {\Sigma }_k^{loc}=\sum _{m\in {\mathcal{N}}_k}{c}_{mk}{\Sigma }_{x_m}.\end{array}$