Problems
9.1 If xi,yi, i = 1,2,…,l, are real numbers, then prove the Cauchy-Schwarz inequality:
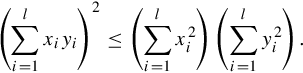
9.2 Prove that the ℓ2 (Euclidean) norm is a true norm, that is, it satisfies the four conditions that define a norm.
9.3 Prove that any function that is a norm is also a convex function.
9.4 Show Young’s inequality for nonnegative real numbers a and b,
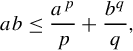
for and such that
9.5 Prove Holder’s inequality for
Get Machine Learning now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

