Machine Learning

11.9 Kernel Ridge Regression Revisited

The kernel ridge regression was introduced in Section 11.7. Here, it will be restated via its dual representation form. The ridge regression in its primal representation can be cast as

$\begin{array}{ll}\hfill \text{minimize with respect to}\mathit{\theta },\mathit{\xi }& J(\mathit{\theta },\mathit{\xi })=\sum _{n=1}^N{\xi }_n^2+C\parallel \mathit{\theta }{\parallel }^2,\hfill \\ \hfill \text{subject to}& y_n-{\mathit{\theta }}^T{\mathit{x}}_n={\xi }_n,n=1,2,\dots ,N,\hfill \end{array}$

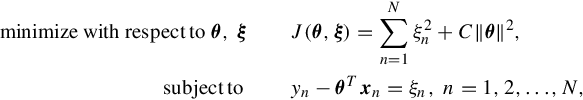  (11.51)

which leads to the following Lagrangian:

$\begin{array}{l}\hfill L(\mathit{\theta },\mathit{\xi },\mathit{\lambda })=\sum _{n=1}^N{\xi }_n^2+C\parallel \mathit{\theta }{\parallel }^2+\sum _{n=1}^N{\lambda }_n(y_n-{\mathit{\theta }}^{\text{T}}{\mathit{x}}_n-{\xi }_n),n=1,2,\dots ,N.\end{array}$

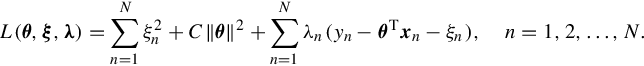  (11.52)

Differentiating with respect to θ and ξ_n, n = 1,2,…,N, and equating to zero, we obtain

$\begin{array}{l}\hfill \mathit{\theta }=\frac{1}{2C}\sum _{n=1}^N{\lambda }_n{\mathit{x}}_n\end{array}$

  (11.53)

and

$\begin{array}{l}\hfill {\xi }_n\end{array}$