Solutions for Chapter 2
- 2.1 Then,
, 
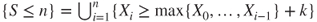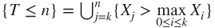, and 
.
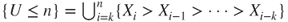- 2.2.a By definition of stopping times,
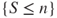and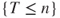 
belong to 
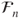. Thus, by definition of the 
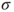-field 
,
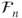- also belong to
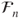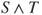, and 
and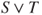 
are also stopping times. Moreover,
- where , and can be written as so that . Hence, , and thus, is a stopping time.
- 2.2.b If and ...
Get Markov Chains: Analytic and Monte Carlo Computations now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
