Description of Sets
Sets are unordered collections of related members in which no members occur more than once. Formally, sets are written with braces around them. Thus, if S is a set containing the members 1, 2, and 3, then S = {1, 2, 3}. Of course, because a set is unordered, this is the same as writing S = {3, 2, 1}. If a member, m, is in a set, S, then membership is indicated by writing m ∈ S ; otherwise, m ∉ S. For example, in the set S = {1, 2, 3}, 2 ∈ S, but 4 ∉ S. To effectively use sets, we should be familiar with some definitions, basic operations, and properties.
Definitions
A set containing no members is the empty set. The set of all possible members is the universe. (Of course, sometimes the universe is difficult to determine!) In set notation:
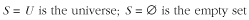
Two sets are equal if they contain exactly the same members. For example, if S 1 = {1, 2, 3}, S 2 = {3, 2, 1}, and S 3 = {1, 2, 4}, then S 1 is equal to S 2, but S 1 is not equal to S 3. In set notation:
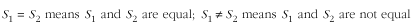
One set, S 1, is a subset of another set, S 2, if S 2 contains all of the members of S 1. For example, if S 1 = {1, 3}, S 2 = {1, 2, 3}, and S 3 = {1, 2}, then S 1 is a subset of S 2, but S 1 is not a subset of S 3. In set notation,
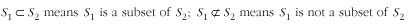
Get Mastering Algorithms with C now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

