Recall that a vector is described by a direction and a magnitude, or length. An eigenvector of a matrix is a non-zero vector that satisfies the following equation:
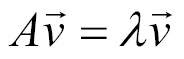
Here,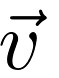 
is an eigenvector, A is a square matrix, and λ is a scalar called an eigenvalue. The direction of an eigenvector remains the same after it has been transformed by A; only its magnitude changes, as indicated by the eigenvalue. That is, multiplying a matrix by one of its eigenvectors is equal to scaling the eigenvector. The prefix eigen is the German ...
