Mastering Machine Learning Algorithms

Analysis of the covariance rule

The covariance matrix Σ is real and symmetric. If we apply the eigendecomposition, we get (for our purposes it's more useful to keep V^-1 instead of the simplified version V^T):

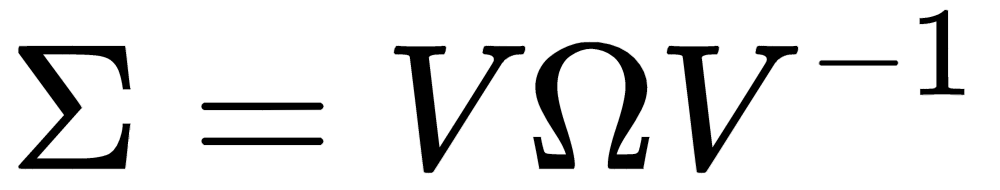
V is an orthogonal matrix (thanks to the fact that Σ is symmetric) containing the eigenvectors of Σ (as columns), while Ω is a diagonal matrix containing the eigenvalues. Let's suppose we sort both eigenvalues (λ₁, λ₂, ..., λ_m) and the corresponding eigenvectors (v₁, v₂, ..., v_m) so that:

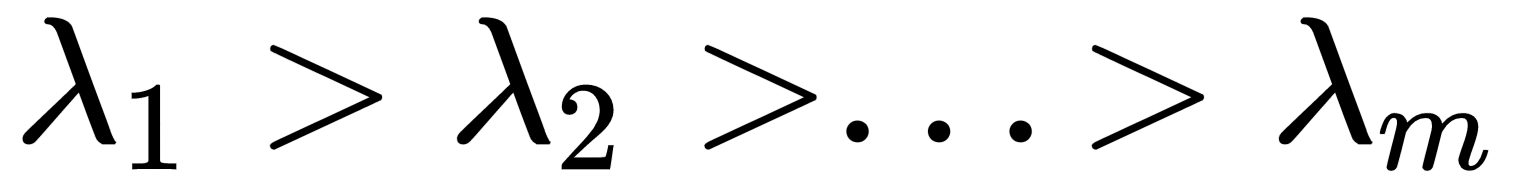
Moreover, let's suppose that λ₁ is dominant over ...