CHAPTER 6
Matrix Algebra
This chapter starts with a brief review of matrix notation and operations. We then explore the application of matrix algebra to risk management.
MATRIX NOTATION
A matrix is a two-dimensional array of numbers, or variables. By convention, the size of a matrix is denoted by the number of rows, and then by the number of columns. For example, the following is a 3 × 2 matrix (pronounced “three by two”):
(6.1) 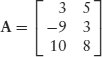
Matrices with only one column are also known as vectors. The following is a 4 × 1 vector:
(6.2) 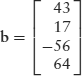
In matrix algebra, we typically refer to ordinary real numbers or variables as scalars. The elements of matrices A and b shown here are all scalars. Traditionally, as here, matrices are denoted by bold letters. Matrices with more than one column are designated by bold capital letters, whereas vectors (i.e., one-column matrices) are designated by bold lowercase letters. Scalars, including the elements of a matrix, are denoted by nonbold lowercase letters.
The various elements of a matrix are differentiated by subscripts, which indicate first the row and then the column of the element. For example:
(6.3) ![]()
In the case of a vector like b, if it does not cause any ...

