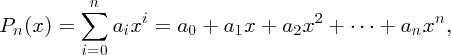Mathematics for Physicists

2 Some basic functions and equations

The discussion of functions of one real variable is continued in this chapter by considering three classes of functions that play an important role in physical sciences. They are: simple algebraic functions; trigonometric functions; logarithms and exponentials.

2.1 Algebraic functions

Here we discuss polynomials and the more complicated functions that can be defined in terms of them.

2.1.1 Polynomials

The polynomial function has the general form

(2.1)

where a_i(i = 0, 1, 2, …, n) are constants, n is a non-negative integer (i.e. including zero), and the symbol Σ means that a sum is to be taken of all terms labelled by the indices 0, 1, 2, …, n. The value of n defines the order (or degree) of the polynomial. The expression x³ − 3x² − 6x + 8 plotted in Figure 1.1 is therefore a polynomial of order 3.

The roots of polynomials are defined as the solutions of the equation

(2.2)

and correspond to the points where a graph of P_n(x) crosses the x-axis. For first-order polynomials, (2.2) is a linear equation of the form

(2.3)

where a and b are constants. This has one root, which is trivially given by x = −b/a.

For second-order polynomials, (