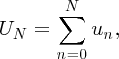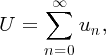Mathematics for Physicists

5 Series and expansions

Perhaps the most important application of the higher derivatives introduced in Section 3.4 is that, provided they exist, they enable functions in the neighbourhood of a given point to be approximated by polynomials in such a way that the accuracy of the approximation increases as the order of the polynomials increases. Such so-called Taylor expansions are useful because the resulting polynomials are often much easier to study and evaluate than the original functions themselves, and they have many applications, as we will see. Firstly, however, we must introduce some basic ideas about series and expansions in general.

5.1 Series

A series is the sum u₀ + u₁ + u₂ + ⋅⋅⋅ of an ordered sequence {u_n} of elements u_n(n = 1, 2, … ). The elements may be numbers, for example , obtained from

(5.1)

or functions, such as u_n = 1, x, x², …  , obtained from

(5.2)

and the sequence may contain a finite number of (N + 1) terms,

(5.3)

or an infinite number of terms

(5.4)

where ...