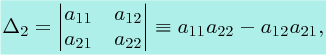Mathematics for Physicists

9 Determinants, Vectors and Matrices

In Chapter 8, we introduced vectors as objects associated with a direction in everyday three-dimensional space and showed how they can be discussed using equations for their three components in a given reference frame. Here we shall show how to extend the number of components to define vectors in spaces of more than three dimensions. This leads to the introduction of matrices, which are two-dimensional arrays that enable vectors to be transformed into other vectors. The properties of matrices are discussed in detail and their uses illustrated in, for example, solving simultaneous linear equations. In the following chapter we continue the discussion of matrices, with applications to vibrating systems and to geometry. Firstly, however, we study related quantities called determinants, which will play a crucial role in this development.

9.1 Determinants

These occur in many contexts and we have already met examples in the discussion of vectors in Chapter 8. From (8.16b), the vector product of two vectors a and b in Cartesian co-ordinates has an x-component (a_yb_z − a_zb_y). Any four quantities a_ij(i, j = 1, 2) combined in this way can be written in the form of a square array, denoted by Δ₂, called a determinant. This is written in the form

(9.1)

where the quantities a_ij(i, j = 1, 2) are called the elements of the determinant. For example,